Crescat Scientia: Outsmarting the Wolf

Monday, April 11, 2011

Outsmarting the Wolf

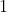
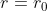
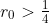
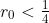
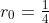
In order to outsmart the wolf, consider your relative angular speed as you swim along concentric circles. Without loss of generality, we may assume the pond has radius $1$ centered at the origin. As you swim along the path $r = r_0$ , the wolf can cover the same central angle more quickly if $r_0 > \tfrac{1}{4}$ , more slowly if $r_0 < \tfrac{1}{4}$ , and at precisely the same speed if $r_0 = \tfrac{1}{4}$ .

From this, we can develop a simple strategy. Swim out near to but just shy of the circle

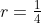
$r = \tfrac{1}{4}$ . Since we can cover the same angle more quickly than the wolf, we may swim in a circle until the wolf is directly behind us. We can cover the remaining distance of slightly more than $\tfrac{3}{4}$ in less than the time it takes the wolf to cover its distance of $\pi$ .

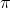
To be more precise, we can successfully implement this strategy of first swimming to

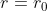
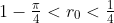
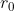
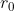
$r = r_0$ exactly when $1 - \tfrac{\pi}{4} < r_0 < \tfrac{1}{4}$ . There is a tradeoff. The smaller the $r_0$ we choose in this interval, the faster we can get to the edge of the pond. On the other hand, the larger we choose $r_0$ , the further away the wolf is when we reach the edge.