Just threw a few more changes in. Angle brackets should be handled better, and the image src is URI encoded so generally it should behave better around weird input.
Even more, I've thrown up installation instructions on the repository's GitHub wiki.
Wednesday, April 27, 2011
Supporting Blogger's New Editor
One of my annoyances with the user script for typesetting LaTeX in Blogger was how it just didn't work with the new editor (otherwise known as issue 7).
No more!
(This post was written in the new editor!)
No more!
(This post was written in the new editor!)
Tuesday, April 26, 2011
LaTeX User Script Updates
Just so you know, I've been able to clean the code for the user script to the point where I think I can easily extend it: in particular, the double escaping is gone and there is much less string manipulation. The script now handles double quotes inside equations properly.
The issues list on GitHub shows what's remaining.
Thursday, April 21, 2011
Trying Out GitHub
I previously wrote about my trivial fix to a user script for LaTeX markup in Blogger.1 Now that I've explored more, I know more options, but I still haven't found a single solution which does everything I would like.
My primary requirement is to easily typeset math which can be read not only on the website, but also from the RSS feed. To that end, the user script mostly works. However, it doesn't look nearly as nice as MathJax.
So, long story short, I believe there are a few more changes I want to make to the user script. I have decided to explore GitHub for code hosting. It's early yet, but it has a very nice interface.
So if you want to follow along, see my new repository.
1Clicking on the original link failed to automatically install the user script. I have fixed it.
My primary requirement is to easily typeset math which can be read not only on the website, but also from the RSS feed. To that end, the user script mostly works. However, it doesn't look nearly as nice as MathJax.
So, long story short, I believe there are a few more changes I want to make to the user script. I have decided to explore GitHub for code hosting. It's early yet, but it has a very nice interface.
So if you want to follow along, see my new repository.
1Clicking on the original link failed to automatically install the user script. I have fixed it.
Tuesday, April 19, 2011
Review: Getting Things Done and Remember The Milk
After setting up Gmail to get things done, I spent some time with the book. I may be late to the party, as everyone seems to know the essentials already.
The gist of the GTD philosophy is to always stay focused on the next action which can be done on any given project. Projects are defined liberally to be anything which consists of a series of one or more actions. For example, renewing my driver's license is a project with at least three steps: find out what documents I need, gather the documents, and finally go to the DMV. Since each step depends on those before, at any point in time only one action can be taken. On the other hand, clearly some projects have many actions which can be taken in parallel.
The premise is that it doesn't make sense to keep all those non-actionable items on your mind. They should be waiting in the wings until you can act on them. Once you consider only the actions you can take now, you can stop worrying quite so much.
Thursday, April 14, 2011
An Easy Classic
You are given twelve marbles, one heavier than the others, and a balance. Find the heavy marble using the balance no more than three times.
Monday, April 11, 2011
Outsmarting the Wolf
In order to outsmart the wolf, consider your relative angular speed as you swim along concentric circles. Without loss of generality, we may assume the pond has radius 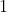 centered at the origin. As you swim along the path
centered at the origin. As you swim along the path 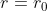 , the wolf can cover the same central angle more quickly if
, the wolf can cover the same central angle more quickly if 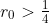 , more slowly if
, more slowly if 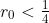 , and at precisely the same speed if
, and at precisely the same speed if 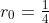 .
.
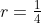 . Since we can cover the same angle more quickly than the wolf, we may swim in a circle until the wolf is directly behind us. We can cover the remaining distance of slightly more than
. Since we can cover the same angle more quickly than the wolf, we may swim in a circle until the wolf is directly behind us. We can cover the remaining distance of slightly more than  in less than the time it takes the wolf to cover its distance of
in less than the time it takes the wolf to cover its distance of 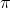 .
.
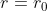 exactly when
exactly when 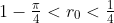 . There is a tradeoff. The smaller the
. There is a tradeoff. The smaller the 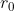 we choose in this interval, the faster we can get to the edge of the pond. On the other hand, the larger we choose
we choose in this interval, the faster we can get to the edge of the pond. On the other hand, the larger we choose 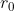 , the further away the wolf is when we reach the edge.
, the further away the wolf is when we reach the edge.
From this, we can develop a simple strategy. Swim out near to but just shy of the circle
To be more precise, we can successfully implement this strategy of first swimming to
Sunday, April 10, 2011
Outsmart the Wolf
Here's a brain teaser (h/t Rob):
You start at the center of a disc-shaped pond. A wolf is at the edge of the pond, and the wolf runs four times as fast as you can swim. He will always run along the edge toward the spot that's closest to where you presently are. How do you get out of the pond without the wolf there to eat you?
You start at the center of a disc-shaped pond. A wolf is at the edge of the pond, and the wolf runs four times as fast as you can swim. He will always run along the edge toward the spot that's closest to where you presently are. How do you get out of the pond without the wolf there to eat you?
Subscribe to:
Comments (Atom)